In making my research open I’ve continually encountered the difficulty of working out what to actually post. My typing speed doesn’t really match the speed at which I write down notes. In order to overcome this I’ve already censored most of the worst mistakes in my handwritten notes: i.e., I’ve spared you all of the crossed-out calculations where I made, eg., a minus-sign error and just written up the corrected notes. But apart from this you are pretty much getting what I’m thinking. There is an exception: I am involved in several projects where my co-authors have, for good reasons, requested I not post on them.
In writing my notes for a wider audience I also attempt to preface each post with some kind of general discussion. This seems to be a useful device, not unlike when using del.icio.us where you are forced to write a description. These little extra tasks seem like a useful mental filing device. Also, I think of the prefaces and tags etc. as a way to enthuse a wider audience to work on the problems I’m working on. (Not entirely clear if this is working yet…)
In this post I’d like to talk about a problem that I’m not really working on, but plan one day to work on if I have an idea. I guess most researchers have these kind of “to do” lists of problems waiting for time/inspiration. I find that these problems take up a lot of mental space (even when I’m not thinking about them directly: eg. “I must remember to think about problem X”) and I’d like to experiment by posting about one of them here in an attempt to clear out this to-do list, so to speak.
The problem/idea I’d like to talk about today is principally motivated by a single figure (Figure 1) in a paper of Cirac and Verstraete.
1. Translation-invariant quantum systems
In this post I’d like to focus on the following setting: imagine we have qubits arranged in a ring. (Everything I’m going to say will also make obvious sense for qutrits in a ring and qudits in a regular lattice etc.) The hilbert space of this system is given by
. There is an obvious symmetry of the ring, namely translation
, which acts on a quantum basis state
,
,
, via
Before we go any further we need to set up a hamiltonian for our system. Let’s agree on what form we’d like this hamiltonian to have. Firstly, physically, any interaction between qubits is likely to be short-ranged, so let’s agree that the hamiltonian for our system should involve only nearest-neighbour interactions (you’ll be able to easily generalise everything I say here to the next-nearest neighbour setting etc.). Secondly, there is this nice translation-invariance symmetry of the ring, so let’s agree that the hamiltonian should be also translation-invariant. Having agreed on these constraints we end up with a hamiltonian which looks like
where the qubits that acts nontrivially on, i.e. it’s support
, are
, where we identify
. Because the system is translation invariant the actual interaction
between qubits
and
is identical to that between
and
, etc. Another way of saying this is that
So (2) actually represents a family of hamiltonians indexed by the size of the system and the nature of the interaction between the nearest-neighbouring qubits. Because of the translation-invariance the actual interactions
between the qubits are completely specified by
which is, in turn, completely specified by a
matrix
via
. Now
is hermitian, so
is as well. We can write any
hermitian matrix as
where are real and
are the Pauli sigma matrices. The coefficient really sets the zero of energy, so we typically set it to
. This leaves
other parameters. Thus, for each
, we have a
-dimensional family of translation-invariant hamiltonians.
A note on : we are going to keep
finite, but we want everything we say to be independent of
. This will facilitate the transition to the thermodynamic limit
, which is often the most interesting setting. If you want you can already think of
as being infinite. But, in this case, you must understand that every statement we make from now on is only true at the level of physical rigour. (This can all be fixed up by working with quasi-local algebras etc. But let’s ignore this for the moment.)
In a sense, the family (2) captures a lot of 1 condensed-matter physics. Many of the celebrated models studied in 1
condensed matter physics are simply points in this
-dimensional space. Examples include the
model and the Heisenberg model. There are many obvious counterexamples to this statement and I leave those to you to enumerate. But the point is that (2) is already a nontrivial interesting class in it’s own right.
Obviously it is actually straightforward to generalise everything I’ve said so far to non-translation invariant systems. In this case the manifold of possible nearest-neighbour systems becomes -dimensional. Also, I leave the generalisations to next-nearest neighbour systems, and higher dimensional systems to you.
2. Ground states
The most fundamental quantum state associated with a quantum hamiltonian is its ground state
, which achieves the minimum in the following variational problem:
Note that the minimum can always be achieved on a (possibly mixed) translation-invariant quantum state. Given a system of the form (2) it is a challenging problem to work out and
. Indeed, for just one point in our
-dimensional space, namely the Heisenberg model, the solution — via the Bethe ansatz — is extremely subtle and complicated.
However, there is a vast simplification available: notice that the energy of a (possibly mixed) translation-invariant quantum state
for a system of the form (2) is given by
where , i.e., the state of just spins
and
, and we’ve exploited the translation invariance. This tells us that the energy of a translation-invariant state
depends linearly only on the reduced density operator of the first two spins.
So this is meant to be motivation for the following
Definition 1 Let
be the convex set of all translation-invariant quantum states, i.e.,
and let
be the convex set
Remark 1 The actual proofs of the facts that
and
are convex is left to you as an exercise.
Note that is a convex subset of the convex set
of two-qubit density operators. Any two-qubit density operator
can be written as
where and
, i.e.,
is a positive semidefinite operator. Notice that the convex set
of all two-qubit density operators is
-dimensional. As a subset of
the convex set
is also
-dimensional.
With these observations in hand we have proved our first result (which is widely known, BTW).
Proposition 2 Let
be a system of the form (2). Then the ground-state energy
for
is given by
This proposition provides us with an interesting corollary: suppose we could understand the -dimensional convex set
. It is a finite set; we might be able to compute its boundary offline using vast computational resources. This would be a one-time cost. Supposing we could specify
, then proposition 2 tells us that we’d have actually calculated the ground-state energy for every single system of the form (2) as the minimisation involved in calculating
is a minimisation of a linear function on a convex set, which is easy. Of course, calculating the ground-state energy for every system of the form (2) is exactly the same as calculating
, so this really isn’t a big surprise. But what I think is helpful here is that the convex set
provides us with a useful construct: proposition 2 tells us that it might be helpful to think about the totality of systems (2) rather than individual systems piecemeal.
Having introduced the convex set , and having motivated its importance in the study of quantum spin systems, I want to actually talk about what it looks like. Because it is a
-dimensional space it is rather difficult to plot. One solution to this is to to plot cross-sections of
. This is exactly what Cirac and Verstaete do in Figure 1 of their paper; they plot the
and
components of all two-qubit density operators (as represented via (9)) in
.
3. Questions
All of this discussion so far has been literature review: all these results are well-known. I now want to discuss a little further some properties of the convex set and put forward some questions about the properties of
.
3.1. Calculating ?
The first question I want to discuss is the problem of calculating . Obviously it is a pretty ugly set: it has curved surfaces and pointy bits. One might well despair at the prospect of providing an equation for its boundary. But I don’t think we should give up hope immediately: there is a precedent for a convex set with similar geometric properties but which admits a rather simple (implicit) parametrisation, namely, the set
. The boundary of this set is defined by two equations:
. When expressed in terms of the coefficients
this tells us that the boundary of
is defined as a real algebraic variety, i.e., as the common zero locus of a quadric surface and a cubic surface. This is the kind of answer I’d like: wouldn’t it be wonderful if the boundary
could be written as the common zero locus of a collection of simple(ish) polynomials? Ok, so it wouldn’t immediately solve the energy-minimisation problem (2) because we’d have to compute a point on a real algebraic variety (tough problem, but in principle solvable), but it would have a certain elegance.
Here is some partial evidence, if you call it that, for why I think the boundary of could be a real algebraic variety. Let
be finite. Now, the extreme points of
, as defined above, are precisely these density operators which satisfy, simultaneously, the following equations
Actually, the last equation is really linear equations in disguise: i.e., if we write
then (13) really stands for the following equations
We could easily spend these equations and rewrite the extreme-point conditions in terms of representative coefficients, i.e., write in terms of the variables
where addition is modulo via
. Thus an extreme point of
is the common zero locus of the equations (11) and (12), when written in terms of
. I’ll write out the first such equation, which is already pretty horrible:
An extreme point of is automatically associated with at least one extreme point of
(but not vice versa), so it must satisfy equations (11) and (12), when written in terms of
. These are quadratic and cubic equations. But there are a vast number of variables. This isn’t quite right: we want the defining equations of an extreme point
to involve only the
numbers (which are, incidentally,
) specifying it as a point in
. This is, in principle, possible to achieve: since an extreme point of
is an extreme point of
once we’ve specified
there can only be one solution to (11) and (12), so all those other variables are not free at all. But this is vile.
I think it would be far more disappointing, but obviously plausible, if the boundary of involved, in the limit
, eg., transcendental functions. I’d still call this a partial victory…
3.2. Supposing we’ve worked out the boundary, now what?
Let’s suppose that we’ve (somehow) worked out an equation, no matter how horrible, for the boundary of . What does this buy us?
Suppose that we know we have a point on the boundary of
and, further, that it is the reduced density operator of the ground state
of some hamiltonian
of the form (2). If the ground state is not degenerate then we know that, given
, we should be able to reconstruct
: suppose not, then there exist two globally different pure states consistent with
with the same energy as the ground state of
. But
has a nondegenerate ground state, hence contradiction.
So knowing is tantamount to knowing
! But this doesn’t help us if we want to get at something like a correlation function
between two separated spins. How can we get at this information? Well, here is a proposal: firstly, all two-point correlators between spin
and
can be calculated from knowing
. The trick is to use knowledge of
to get at
without needing to solve exponentially many simultaneous equations. I would like to think this can be done sequentially with bounded space and computational requirements using semidefinite programming along the lines of the following method.
- Take
and
(both equal, and known by assumption). Solve the semidefinite program:
where
is some hermitian matrix (to be chosen later). Now, even for ground states of gapped hamiltonians there can be many feasible points for the above SDP: it is only the global state which needs to be unique, but there could be many states consistent with any subset of the spins.
- Trace out qubit
: this gives us the reduced density operator
. Take
(known, by assumption) and solve the above SDP to get
. Then trace out qubit
.
- Repeat until the reduced density operator
is obtained. At this point all correlators
can be calculated.
So the problem here is in the first step where we need to choose a single point as the “correct” state consistent with
and
. (This is what the matrix
is doing…) I don’t know at the current time what principle could conceivably do this short of working out
and then a posteriori choosing the correct extension state
at each step…
So this method seems great if we know we have a point on the boundary corresponding to the ground state of a nondegenerate system. But what about systems with degenerate ground states (like critical systems)? I’m not sure: there can now be many solutions to the above SDP at each step…
Another question is to actually prove the exponential decay of correlations for gapped nondegenerate systems from this method (why? Well, another proof would be kind of interesting…) This might be possible because of the sequential nature of the method presented above: somehow there should be a degradation of information as we iterate the method.
3.3. Approximate results
We can approximate from within using trial states, like finitely correlated states/matrix product states: any reduced density operator of a translation-invariant quantum state is a point in
. We can approximate
from the outside using lower bounds for the ground-state energy: a lower bound provides an overestimate for the minimisation of proposition 2: by varying over all the hamiltonians
of the form (2) we can get points outside
.
Suppose we approximately have a point on the boundary of : what can we say about correlations, etc.? This is roughly equivalent to asking how robust the method of the previous subsection is to perturbations.
3.4. Non-translation invariant states
The set of of all
nearest-neighbour reduced density operators of states of
qubits forms a convex set. Extreme points correspond to ground states of nearest-neighbour hamiltonians, just like for translation-invariant systems. Given an extreme point, just like for translation-invariant systems, the SDP method of above ought to provide a method to obtain correlation functions.
Now one related problem, which is probably on a lot of people’s hit list, is the following. Suppose we have some non translation-invariant nearest-neighbour hamiltonian for
qubits. Is there a method which obtains an estimate of the ground-state energy of
, guaranteed to be correct to some additive constant factor, which uses only polynomial space and time resources (in
). (If “qubits” are replaced by “qutrits” then I think most people would agree that this is probably false, i.e. the problem is probably(?) QMA-complete…) This is equivalent to getting a point in
which is within a distance
of the boundary (measured using trace norm).
[Update 13/3/2009: fixed incorrect assertion concerning uniqueness of feasible points of semidefinite programs.]
[Update 21/3/2009: fixed missing equation (2).]
Hi Tobias
A stray google hit lead me to your page. Nice articles! Thanks for all the work!
Let me comment on this post. Some time ago, I thought a bit about . Ever since, it’s called the “evil convex set” between Jens and me. The name should be indicative of my success in learning anything about it. 🙂
. Ever since, it’s called the “evil convex set” between Jens and me. The name should be indicative of my success in learning anything about it. 🙂
To turn my uninformed pessimism about into educated pessimism, let me argue why I think it’s unlikely that
into educated pessimism, let me argue why I think it’s unlikely that  is an algebraic variety (at
is an algebraic variety (at 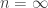 ). Indeed, one should be able to use the same argument as the one Fannes, Nachtergaele, Werner employed to show that the ground state of the Heisenberg model is not finitely correlated.
). Indeed, one should be able to use the same argument as the one Fannes, Nachtergaele, Werner employed to show that the ground state of the Heisenberg model is not finitely correlated.
In this context, I would summarize the argument as follows. Assume that is the common locus of the zeros of a set of polynomials with coefficients in, say, the real algebraic numbers. Now, the Hamiltonian of the Heisenberg model has algebraic matrix elements. Thus the problem of finding its ground state energy density is stated completely in algebraic terms. But the energy density is (apparently)
is the common locus of the zeros of a set of polynomials with coefficients in, say, the real algebraic numbers. Now, the Hamiltonian of the Heisenberg model has algebraic matrix elements. Thus the problem of finding its ground state energy density is stated completely in algebraic terms. But the energy density is (apparently) 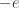 , so transcendental. One should start to worry.
, so transcendental. One should start to worry.
More precisely, denote the 16 real coordinates of a Hermitian matrix on a two-qubit space by . Say there are
. Say there are  polynomial equations
polynomial equations  defining
defining  . Let’s bring the energy into the picture, by passing to
. Let’s bring the energy into the picture, by passing to  with coordinates
with coordinates  and a further constraint
and a further constraint  . Next, we hope that one can identify all critical points of the energy expectation on
. Next, we hope that one can identify all critical points of the energy expectation on  by means of Lagrangian multipliers. I.e., we look at the variety
by means of Lagrangian multipliers. I.e., we look at the variety 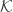 in
in  with coordinates
with coordinates  and extra constraints
and extra constraints
The projection of
of 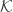 onto the
onto the  -axis should consist of all energies obtained at critical points of
-axis should consist of all energies obtained at critical points of  on
on  . But by the Tarski-Seidenberg theorem,
. But by the Tarski-Seidenberg theorem,  is semi-algebraic. Because the algebraic numbers form a closed real field, the boundary points of
is semi-algebraic. Because the algebraic numbers form a closed real field, the boundary points of  are algebraic. This must in particular be true for the minimal and maximal energies.
are algebraic. This must in particular be true for the minimal and maximal energies.
Is this a proof? Not quite. One should spend a minute checking that (or when) algebraic varieties are benign enough that Lagrangian multipliers are guaranteed to find all critical points. Also, my knowledge of real algebraic geometry is rather pathetic, so I might have overlooked something basic.
All this, of course, makes the evil convex set all the more interesting.
Is there a way to preview/edit your own comments?
In order to get all the LaTeX in my reply to work, I had to set up a dummy blog. 🙂 Not too efficient.
(And now that I did submit it, I find a typo in the first sentence… “led me to your page”, of course).
Hello!
I have trouble seeing some of the equations. For example, after the second paragraph in section 1,
“hamiltonian which looks like… ”
and there I asee nothing.
Do you know what to do?
Thanks,
Orr
Dear David,
Many thanks for your comment! Your argument is really nice (I’m especially impressed by how you leveraged FNWs key observation)! It’s also pretty persuasive: I feel much more pessimistic about the hopes of being algebraic… 😉 Oh well… Evil convex set is a great name!
being algebraic… 😉 Oh well… Evil convex set is a great name!
But I would still find it interesting if were the common zero locus of some easily specified simultaneous equations (perhaps involving exp, etc.?) though…
were the common zero locus of some easily specified simultaneous equations (perhaps involving exp, etc.?) though…
On the comments: alas, as far as I can see, wordpress doesn’t allow comment previewing. I am thinking of hosting this blog locally, in which case I can install a plugin to allow this. As a partial fix: one suggestion would be to write comments in plain latex and use Luca Trevisan’s wonderful script: http://lucatrevisan.wordpress.com/latex-to-wordpress/
and just paste the result into the comment box. This ought to work…
Dear Orr,
Many thanks for spotting this! It was actually a weird typo that I’ve now corrected.
Welcome! You might have that typo also after paragraph 3 in section 1 of the previous post.
Dear Orr,
Just found your second comment: I’ve fixed up the missing equations problem. Many thanks for spotting this!
Hi Tobias,
Let me preface this by saying that these may be very naive comments, since I haven’t really looked at this problem before.
It seems to me that the set C is so messy because it contains states which are eigenstates of the translation operator having different eigenvalues. As a translationally invariant Hamiltonian has a translationally invariant ground state, we know that states containing coherent superpositions of two or more eigenstates of T having at least two distinct eigenvalues cannot be part of the ground state. In fact, these are the only states which cannot be part of the ground state. So this would seem to suggest that the set C has a simple representation in terms of the Boolean union of several easily paramterised sets.
Actually, since the ground state cannot contain coherent superpositions of states having different eigenvalues with respect to T, this means that these cross terms in the density matrix must be zero. If the density matrix is written in a basis such that each of the computational basis states are eigenvectors of T, and states with the same eigenvalue are grouped together, then the set C is simply the set of all block diagonal density matrices whose blocks operate only on states having the same eigenvalue with respect to T. For any dimensionality of the local systems this should be fairly easy to work out.
Perhaps I have missed a subtelty somewhere, but I would have thought this approach viable.
Dear Joe,
Many thanks for your comment!
Am I correct in understanding what you are saying as: since the ground state of a translation invariant hamiltonian is also an eigenstate of the translation operator, we should spend this symmetry in order to simplify the analysis? This is definitely true, but I fear it doesn’t buy us a great deal: there are, roughly speaking,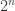 unknowns for a general ground state, and the translation invariance condition only gives us, roughly speaking
unknowns for a general ground state, and the translation invariance condition only gives us, roughly speaking  equations. Another way of saying this is that the eigenvalues of the translation operator are highly degenerate: if the system consists of
equations. Another way of saying this is that the eigenvalues of the translation operator are highly degenerate: if the system consists of  spins the translation operator
spins the translation operator 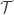 has eigenvalues
has eigenvalues  ,
,  , and each eigenvalue has degeneracy, roughly speaking,
, and each eigenvalue has degeneracy, roughly speaking,  . So, unfortunately, diagonalising
. So, unfortunately, diagonalising  in the diagonal basis of
in the diagonal basis of 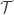 will only reduce the complexity of the problem only slightly…
will only reduce the complexity of the problem only slightly…
Sincerely,
Tobias
Hi Tobias,
That is more or less what I meant except that I assume we keep the partial trace. Perhaps a much easier way to see it is the following (please excuse the lack of latex, I don’t know how to use it in wordpress):
Let \rho be density matrix corresponding to the ground state of the Hamiltonian. Let \rho_AB be the partial trace of the system over all spins except A and B, and similarly let \rho_A and \rho_B be the partial trace over all spins other than one spin, A or B respectively.
What form can \rho_AB take? Well there are 15 free parameters (corresponding to the weight of each of the 15 Pauli matrices). However, we do know that this state must be translationally invariant. This means that \rho_A and \rho_B must be equal. But as each of these is a single qubit density matrix the resulting equality introduces dependencies for 3 of the parameters in \rho_AB, so we end up with only 12 free parameters.
Joe
I forgot to mention that translationally invariant Hamiltonians have the same number of free parameters, since the local fields must be equal.
Dear Joe,
Many thanks for your comment!
What you describe is certainly one approach to the problem: one characterises the set of all possible via the constraint that
via the constraint that 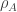 and
and  must be equal. However, there are more (in fact, infinitely many more) constraints. Consider the singlet state
must be equal. However, there are more (in fact, infinitely many more) constraints. Consider the singlet state  . This satisfies the constraints you describe, but it cannot be the reduction of any translation invariant state: the reason is due, if you like, to entanglement monogamy. To use a more pedestrian explanation: there are more constraints coming from the fact that
. This satisfies the constraints you describe, but it cannot be the reduction of any translation invariant state: the reason is due, if you like, to entanglement monogamy. To use a more pedestrian explanation: there are more constraints coming from the fact that  needs to come from a legal quantum state on 3 qubits
needs to come from a legal quantum state on 3 qubits 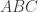 and we need that
and we need that  . This generates more constraints (which rule out the singlet). Then we need to deal with the fact that
. This generates more constraints (which rule out the singlet). Then we need to deal with the fact that  needs to come from a legal quantum state on 4 qubits
needs to come from a legal quantum state on 4 qubits 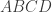 etc. etc.
etc. etc.
However, this approach does generate outer approximations to the “evil convex set”…
Sincerely,
Tobias
Yes, that seems to be a subtlety I was missing. However, I would think we could extend the approach to include correlations. Since we can consider the density matrix of that entire subsystem
we can consider the density matrix of that entire subsystem  . Now,
. Now,  . Now, correlations must be translationally invariant, so applying the translational invariance condition yields a lot more information, and we can exclude the singlet state.
. Now, correlations must be translationally invariant, so applying the translational invariance condition yields a lot more information, and we can exclude the singlet state.
Dear Joe,
I’m certainly coming to the conclusion that your suggestion is a pretty decent way to proceed (I don’t have any better ideas)… I’m convinced, however, thanks to David Gross’ observations, that to fully describe the boundary of we’d still need to solve potentially infinitely many constraint equations. (After all, the singlet example can be generalised to apply to the 4 qubit setting using, eg., a GHZ state: this can’t be extended to 5 qubits…) Nevertheless, there is some hope that systematic approximations can be obtained via this approach…
we’d still need to solve potentially infinitely many constraint equations. (After all, the singlet example can be generalised to apply to the 4 qubit setting using, eg., a GHZ state: this can’t be extended to 5 qubits…) Nevertheless, there is some hope that systematic approximations can be obtained via this approach…
Dear Tobias,
I your objection misses a subtlety here. Since we are only interested in , the GHZ states on 4 (or 3) qubits become identical to GHZ states on N qubits, since $latex \mbox{Tr}_{AD}(|\mbox{GHZ}_4 \rangle \langle \mbox{GHZ}_4|) = 1/\sqrt{2}(|00\rangle\langle 00| + |11\rangle\langle 11|), which is not only a translationally invariant state, but is the ground state of the Ising interaction. So while the 4 qubit density matrix includes states which are not translationally invariant, the partial trace leading to the reduced density matrix that we are actually interested in equates these entangled states to mixed states which are valid.
, the GHZ states on 4 (or 3) qubits become identical to GHZ states on N qubits, since $latex \mbox{Tr}_{AD}(|\mbox{GHZ}_4 \rangle \langle \mbox{GHZ}_4|) = 1/\sqrt{2}(|00\rangle\langle 00| + |11\rangle\langle 11|), which is not only a translationally invariant state, but is the ground state of the Ising interaction. So while the 4 qubit density matrix includes states which are not translationally invariant, the partial trace leading to the reduced density matrix that we are actually interested in equates these entangled states to mixed states which are valid.
Joe
Dear Tobias,
I your objection misses a subtlety here. Since we are only interested in , the GHZ states on 4 (or 3) qubits become identical to GHZ states on N qubits, since
, the GHZ states on 4 (or 3) qubits become identical to GHZ states on N qubits, since  , which is not only a translationally invariant state, but is the ground state of the Ising interaction. So while the 4 qubit density matrix includes states which are not translationally invariant, the partial trace leading to the reduced density matrix that we are actually interested in equates these entangled states to mixed states which are valid.
, which is not only a translationally invariant state, but is the ground state of the Ising interaction. So while the 4 qubit density matrix includes states which are not translationally invariant, the partial trace leading to the reduced density matrix that we are actually interested in equates these entangled states to mixed states which are valid.
Joe
Ok, I seem to have messed up the latex. Feel free to fix it.
Dear Joe,
I fixed the latex in your comment. For help on using latex in wordpress check out
It’s just occured to me that dealing with a 4 spin system and then tracing out the end to spins (as I mentioned above) should contain all the structure of the full chain, since any entangled state of these four spins will result in the same reduced density matrix on the two central spins as some translationally invariant state of N qubits.
Concerning the GHZ example: what you say is correct, the two-qubit reduced density operators it gives rise to can be found from other global states. But, obviously, the GHZ cannot be the reduced density operator of a larger translation-invariant state.
However, the example below will show that there are 2-qubit reduced density operators which can come from 4 qubits but not infinite qubits.
In the case of a chain of 4 qubits there are several ways to see that the middle two spins cannot contain the full complexity of the infinite chain. One way is to study the ground-state energy of a spin system on 4 spins, and the equivalent system on an infinite chain.
Consider an antiferromagnetic heisenberg spin chain with hamiltonian
 . The ground-state energy of such a system only depends on the two-qubit reduced density operators (RDOs) of the neighbouring qubits. Further, the energy depends linearly on these RDOs. Thus the ground state energy is the minimum achievable amongst all two-qubit RDOs compatible with 4 qubit global states. The ground-state energy per spin of the antiferromagnetic spin chain is -2. Let’s write the corresponding 2-qubit RDO of the ground state as
. The ground-state energy of such a system only depends on the two-qubit reduced density operators (RDOs) of the neighbouring qubits. Further, the energy depends linearly on these RDOs. Thus the ground state energy is the minimum achievable amongst all two-qubit RDOs compatible with 4 qubit global states. The ground-state energy per spin of the antiferromagnetic spin chain is -2. Let’s write the corresponding 2-qubit RDO of the ground state as  .
.
In the infinite spin case, if the 2-qubit RDOs really could each be then that would imply that the ground-state energy per spin could be as low as -2. However this is not the case. The ground-state energy of the AF heisenberg chain is
then that would imply that the ground-state energy per spin could be as low as -2. However this is not the case. The ground-state energy of the AF heisenberg chain is  , which is strictly greater. Thus we conclude that
, which is strictly greater. Thus we conclude that  *cannot* be compatible with a translation invariant quantum state on large numbers of qubits.
*cannot* be compatible with a translation invariant quantum state on large numbers of qubits.
Indeed, the AF heisenberg model on any finite number of spins gives rise to two-qubits RDOs which cannot be RDOs of an infinite number of spins. (This is essentially David Gross’ observation above.)
Hi Tobias,
Thanks for your reply. Sorry for wasting your time. I can certainly see the problem now, but it still doesn’t seem beyond hope to parameterise the density matrices which correspond to translationally invariant states on infinite chains. One way to go about this would be to consider relationships between coefficients of Pauli operators in the density matrix. For example, in the 4 qubit case, we have required XXII = IXXI = IIXX, but it neglects the fact that XIII + XIIX + XIIY + XIIZ = IXII + XXII + YXII + ZXII etc.
Since by definition applying the translation operator T to the ground state stabilizes the state then for a Pauli operator P on N qubits the coefficient of P should be equal to the coefficient of . If we consider a two-qubit density matrix we get the constraints:
. If we consider a two-qubit density matrix we get the constraints:
P(I + X + Y + Z) = (I + X + Y + Z)P
for P = I,X,Y,Z.
Each particular person has the right to acquire knowledge and plenty of organizations supply their help to verify that every achieves efficient education https://math-problem-solver.com/ .
Systematic treatment of indeterminate simultaneous linear congruences (Chinese remainder theorem).
Hello Tobias,
Could you please fix the missing equation (9)? I have tried to refresh several times, but it is not rendering. Thanks!
I’ve fixed it.
Sincerely,
Tobias
Thank you, Tobias. By the way, I wonder why the normalization is 1/16 given that the Pauli matrices are traceless?
the pauli matrix sigma^0 is the identity and not traceless.
Sincerely,
Tobias
Just one more friendly reminder that equations (11), (12), and (13) are also missing.
fixed
[…] 正如Prof. Tobias J. Osborne所说,每个做学术的人心里都会有个列表,里面记录的都是“我想研究的,但是一时没有什么头绪,不过如果把手头的工作都做完了的话一定会做”的课题。虽然这样子,但是心里面还是经常会惦记着这些问题,还需要时常提醒自己“一定不要忘了”。解决这种一直担忧着的烦恼的办法之一就是把目前关于这个问题的思考记录下来,一来免于忘记目前的思考乃至于问题本身,二来也算是可以更好的卸下这个问题带来的担子以便完成手头的工作,三是如果这个潦草的笔记能够吸引其他人思考这个问题或者帮助其他正在思考这个问题的人就再好不过了。 […]