Topological order for mixed states

In this post I’d like to take the opportunity to talk about the problem of defining what is meant by topological order at finite temperature. I hope to convince you that there is a natural, operationally well motivated, definition for what this means.

But first let’s recall what is meant by topological order.

There appear to be quite a few related yet not quite obviously equivalent definitions floating around: some define it with reference to edge modes, some define it in terms of the topological entanglement entropy, and yet another definition concerns ground state degeneracy on a surface of genus .

The definition I like the most, and which I’ll exploit for the rest of this post is due variously to Xiao-Gang Wen and coauthors and is in terms of local deformation operations. (I’m using the terminology of “local deformation operations” (LDO) instead of Wen’s “LU” to avoid some confusion later on.) To explain this definition we’ll need to work with infinite quantum lattice systems.

Topological order and disorder

Topological order is a curious property possessed by some special quantum many-body systems. While there is no universally accepted definition of the property a good prototype is that a system is topologically ordered if it: (a) has a degenerate ground eigenspace separated by a gap 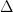from the rest of the spectrum; and (b) each state 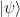in the ground eigenspace looks “locally” the same as any other. That is, the measurement statistics of any localised observable cannot distinguish between any of the degenerate ground states. This definition isn’t rigourous, and there are some necessary refinements. (Other definitions involve the degeneracy of the model on surfaces of arbitrary genus or use topological entropy notions. I don’t want to discuss this here.)

Topologically ordered systems are interesting for many reasons ranging from their counterintuitive properties, to the possibility of using them as robust quantum memories to store quantum information. This is because some topologically ordered systems are extremely stable to (local) noise: since local observables can’t distinguish between different ground states, neither can any source of local decoherence, so one might expect it to take a long time for such systems to decohere. The story is more subtle than this, however, and I’ll simply refer you, for example, to this and this and this for further details and discussion.

Topological order is not the only property which is a consequence of quantum coherence, there are plenty more. Another particularly well-known example is (Anderson) localisation: when a system of propagating particles is subjected to a weak statically disordered external field the quasiparticle wavefunctions become localised and all diffusion is suppressed. (I refer you to my previous post here for further discussion.) A caricature of this phenomenon is then that static disorder eliminates the possibility of establishing long-range quantum correlations in a localised system.

Now topological order is the consequence of the propagation of correlations over large distances (see this paper by Bravyi, Hastings, and Verstraete for a proof). So, combining the naive intuition for the localisation phenomenon with the requirements of correlation propagation one is tempted to conjecture that the addition of static disorder will destroy topological order for any system. If true this might be bad news for topologically ordered systems as disorder is always present in naturally occurring systems. In response to this observation one might argue that recent results on the stability of topological order shows that we needn’t be worried, and this is indeed true when we can engineer our systems so that the disordering field is uniformly small with respect to the system hamiltonian. However, typical disorder is gaussian distributed in strength and this violates the conditions of these studies (with high probability, for large system sizes), so they aren’t directly applicable without modification. This is ok, though, as long as there is some kind of “bulk mobility gap” which allows a disentangling process to be carried out quickly relative to the system size. Obviously, much remains to be done to prove the existence of such a gap for simple toy models. (This explanation suggests a nice possible future research topic: use a modification of the bootstrap argument of Bravyi and Hastings to prove the existence of a bulk mobility gap for a simple toy model.)

In a recent paper with Dimitris Tsomokos and Claudio Castelnovo we investigate the conjecture that topological order is destroyed by disorder for a collection of simplified toy models and more realistic disordered systems. We show that, surprisingly (at least, initially, for me), topological order is not destroyed at all, in fact, quite the opposite! There exist topologically ordered systems that, once exposed to external fields enter a phase with no topological order. However, if you add a certain amount of static disorder they can reenter a topologically ordered phase. The general picture is far from clear: we found that there exist topologically ordered systems robust to any amount of disorder, and some that are robust only to a constant amount.

There is actually intuitive explanation for why disorder might be a helpful thing. This explanation is really only valid for small external fields, but I found it rather useful. The idea is as follows. Suppose we consider the original Kitaev toric code (a very simple topologically ordered system). Here the excitation spectrum consists of a four-fold degenerate ground state separated by a gap from the first excited states, each of which correspond to stationary anyons.

When a uniform magnetic field is added this band of excited states is broadened and thus the anyons acquire a momentum and are no longer stationary: localised anyons can propagate ballistically throughout the sample at some lattice momenta. When the magnetic field is small the system has a spectral gap and the system retains topological order as the ground state can be adiabatically connected with the original toric code model. As the magnetic field is increased the spectral gap is closed and topological order is lost.

One can physically understand this loss of topological order as being due to a process of quasiparticle creation and annihilation: the ground state in the presence of the magnetic field can be understood as equivalent to that of the clean model in a sea of virtual quasiparticles which are being spontaneously created, propagated a distance proportional to the inverse gap (which provides the fundamental lengthscale of the system), and then spontaneously annihilated. Naturally, as the magnetic field is increased and the gap is decreased the virtual anyons can propagate further, to the point where they can travel around the torus. At this point they can effect virtual transitions between the 4 degenerate ground states and coherence in the ground-state sector is lost.

Now, if we subject the system to a disordered magnetic field one expects that the quasiparticle wavefunctions will be localised. This will have a profound effect on the propagation of virtual anyons as again, one can understand the ground state of the model in the presence of a magnetic field and quenched disorder as equivalent to that of the original toric code model in a sea of virtual propagating anyons. This time, however, thanks to the localisation the anyons cannot propagate very far before they are annihilated. Hence, even though the spectrum of the disordered model fills with low-lying eigenvalues, these eigenvalues correspond to localised anyons which cannot propagate more than a short distance. Thus the system retains topological order.

Wissenschaftskolleg zu Berlin, 2010.